[数学1 クラス対象(金曜日5限)]
以下、余計なことを書きすぎたので最後の2つについては書けませんでした。
またどこかでかきます.
次回はラグランジュの未定乗数法です.
特異点
ある方程式 $F(x_1,x_2,\cdots,x_n)=0$ を満たす点 $(x_1,x_2,\cdots,x_n)$ の中で、
$$\begin{cases}F_{x_1}(a_1,a_2,\cdots,a_n)=0\\F_{x_2}(a_1,a_2,\cdots,a_n)=0\\\cdots\\F_{x_n}(a_1,a_2,\cdots,a_n)=0\end{cases}$$
を満たす点のことを特異点といいました.
勾配ベクトル
勾配ベクトルは以前やりましたが、ここでは
関数 $F(x,y)$ $F(x,y,z)$ に対してその役割と性質をまとめておきます.
関数 $z=F(x,y)$ $w=F(x,y,z)$ があったときにその勾配ベクトルとは
$\text{grad}(F)(x,y)=(F_x(x,y),F_y(x,y))$,
$\text{grad}(F)(x,y,z)=(F_x(x,y,z),F_y(x,y,z),F_z(x,y,z))$
などとなり、それぞれ、2次元上のベクトルと3次元上のベクトルになります.
これを勾配ベクトルといいます.
また、このとき、このベクトルたちは各点に与えられているので、
そのような状況をベクトル場、この場合は関数の勾配を与えているので
勾配ベクトル場とよばれます.
この場という言葉は物理(ヒッグズ場とか重力場とか)でも出てきますが、
この場合と同じような意味合いです.
空間の上の各点に一斉に与えられる一つの状態を表しています.
例えば $f(x,y)=x^2+y^2$ の場合の $\text{grac}(f)(x,y)=(2x,2y)$ の
様子は授業でもやりましたが、以下のようになります.
放射状になっているのは、各点において関数 $f(x,y)=x^2+y^2$ が増える方向が外向きであるからです.
もう一次元落として考えれば、$f(x)=x^2$ も、導関数 $f'(x)=2x$ であり、絶対値が大きくなる
に従って2倍のスピードでその傾きが増えています.
関数の接平面の傾きがだんだんと急になっていることを表しています.
また、同心円はこれらのベクトルに一斉に直交しますがその円は $f(x,y)$ を
一定とする集合 $V_c=\{(x,y)|x^2+y^2=c\}$ となる等高線を意味します.
皆さんにやってもらったのは $f(x,y)=xy$ でしたが、
その時は以下のようになりました.
矢印をつなげて書けば
$y=-x$ の近くの点から矢印をたどっていくと、
まず、原点方向に向かって流れ、向きを変えて
今度は $y=x$ の近くの点を通って無限大に流れていきます.
これは、馬の鞍の腹の方から登っていき、背中を通って馬の頭(もしくは尻)の方を
だどって登っていくことに対応しています.
ちなみに原点では矢印が有りませんからどこにも向かいません.
止まったままです.
このような点は$F_x(a,b)=F_y(a,b)=0$ ですから、関数 $z=F(x,y)$ の
臨界点であることに注意しましょう.
授業中に等高線も描きましたね.自分でももう一度やってみてください.
関数 $w=F(x,y,z)$ においても勾配ベクトル場があります.
関数のグラフは4次元 $(x,y,z,w)$ の中に入っている3次元の物体なので見えませんが、
その等高面 $F(x,y,z)=c$ は3次元の中の曲面として見ることができます.
それは等高面なのでそれと垂直な方向に勾配ベクトルが向いています.
例えば、$F(x,y,z)=x^2+y^2+z^2$ のときは、等高面 $x^2+y^2+z^2=c$ は同心球
のことで、勾配ベクトル場は $\text{grad}(F)(x,y,z)=(2x,2y,2z)$ ですので、
上と同様一点から矢印が湧き出しています.
一般の関数 $z=F(x,y)$ や $w=F(x,y,z)$ は臨界点が複数入り乱れ、その周りで
$\text{grad}(F)$ が動き回っていることになります.
$z=F(x,y)$ において、非退化な(ヘッシアンが消えてない)臨界点の周りでの
$\text{grad}(F)$ の"様子"は上の、 $x^2+y^2$(湧き出し)もしくは、
$xy$ (馬の鞍)もしくは、$-x^2-y^2$ (吸い込み) のどれかに実はなっています.
退化した臨界点に関する臨界点では、状況は複雑で、ベクトル場を自分で
描いてみるとよくわかると思います.
以下、実際の具体例について、授業で取り上げた関数についての話です.
関数 $F(x,y)=x^3+y^3-3xy$ の話
例題6-1(1)
$F(x,y)=x^3+y^3-3xy=0$
は、デカルトの正葉線と呼ばれます.
のような集合ですが、$F_x(x,y)=3x^2-3y=0$ かつ $F_y(x,y)=3y^2-3x=0$
は、$(x,y)=(0,0)$ のみです.この点において接線が存在しないことになります.
これは、$z=F(x,y)$ の関数の $z=0$ での等高線とも考えられます.
前回の陰関数定理を用いれば $F_y=3y^2-3x\neq 0$ のとき、
つまり、$(x,y)=(0,0)$ もしくは $(\sqrt[3]{4},\sqrt[3]{2})$
以外では、各点は、その点の十分小さい周りにおいて、$x$-軸から関数の形をしている
ことがわかりました.
これは、$y$ に関する3次方程式 $y^3-3xy+x^3=0$ の解として、
この集合をみると分かるように、$x<0$ もしくは $x>\sqrt[3]{4}$ のとき、
この3次方程式は1つの実数解があり、$0<x<\sqrt[3]{4}$ のとき
3つの異なる実数解があります.
これは $x,y$ の変数を入れ替えてもおなじことです.
また、例題6-5(1) でも同じ式からなる集合
の陰関数を $y=\varphi(x)$ とし、$b=\varphi(a)$ において、
$\varphi'(a)=-\frac{F_x(a,b)}{F_y(a,b)}=-\frac{a^2-b}{b^2-a}$
であり、$\varphi'(a)=0$ となるような点は $a^2-b=0$ となり、
そのような点は $(a,b)=(0,0)$ もしくは $(\sqrt[3]{2},\sqrt[3]{4})$
となる.
例題6-4から
陰関数の臨界点での2階微分は以下のようになります.
授業では最後の方の計算を間違えていました.
$\varphi''(a)=-\frac{F_{xx}(a,b)}{F_y(a,b)}$ であるから、
$F_{xx}(x,y)=6x$より
$\varphi''(\sqrt[3]{2})=-\frac{6\sqrt[3]{2}}{3\sqrt[3]{4^2}-\sqrt[3]{2}}=-\frac{6\sqrt[3]{2}}{5\sqrt[3]{2}}=-\frac{6}{5}<0$
となりますので、$(\sqrt[3]{2},\sqrt[3]{4})$ では $x$-軸から見て極大になっている
ことがわかります.
また、この関数を $z=F(x,y)$ なる関数として、グラフを作ってみると下のようになります.
なんとなく人間工学に基づいて設計された椅子のような形をしていますね.
この椅子、この絵からはよくわかりませんが、臨界点は $(0,0)$ と $(1,1)$ あります.
$(1,1)$ では極小値ですが、 $(0,0)$ ではいわゆる馬の鞍になっています.
座り心地がよさそうですね.3Dプリンターで作ってみたいくらいです.
もし家具屋でこのような曲面に出会ったら触って臨界点の位置を実感してください.
馬の鞍というのは、授業でもやりましたが、局所的に$z=xy$ となっている点です.
$z=x^2-y^2$としても定義域の座標変換で同じ形の臨界点が表れます.
そのような関数のグラフの $z=0$ での切り口は$x=0$ もしくは$y=0$ となる2つの直線です.
$F(x,y)=x^3+y^3-3xy$ の例では、$(0,0)$ の付近ではこの関数の高次の項 $x^3+y^3$ を
無視して考えます.
すると、主要項は $-3xy$ であり、大体馬の鞍だというわけです.
それが、$F(x,y)=0$ が原点で周りでクルンとなっている理由なわけです.
いまは $z=-3xy$ とは違い、3次の項のせいで、原点から遠くの方で2つの線はつながっています.
ちなみに $F(x,y)=x^3+y^3-3xy$ の勾配ベクトル場を描いて、矢印を
滑らかに繋いでやると下のようになります.
$(1,1)$ において、矢印がわき水のように湧き出していますね.
原点では局所的にさっきの $xy$ ベクトル場と同じような状況になっています.
デカルトの正葉線は関数 $z=F(x,y)$ の $z=0$ での等高線なわけですが、
この、ボールペンの試し書きのような曲線は、
他の高さではどうなっているでしょうか?
($z$ 座標は高さととらえることもできますが、時間と考えても面白いです.)
$V_c=\{(x,y)\in{\Bbb R}^2|F(x,y)=c\}$ として、$V_c$ の絵を
追いかけていきましょう.
$V_0$ は上のボールペンの試し書きでした.
$V_1$ は下のような曲線です.
交差が外れていますね.
$V_{-0.5}$ のときは下のようになります.
卵が出てきましたね.
そして $z$ をさらに下げていくと、この卵は $(1,1)$ に向かって小さくなって、
$z=-1$のときに一点になります.$F(1,1)=-1$なので、丁度極小値の時なわけです.
これは、$x^3+y^3-3xy+1=(x+y+1)(x^2+y^2-xy-y-x+1)$ のように因数分解されて、
もう一つの等高線の成分は直線になります.
$x^2+y^2-xy-y-x+1=0$ の方は、$(2x-y-1)^2+3(y-1)^2=0$ と書き直せるので、
実数の範囲では$(x,y)=(1,1)$ しかありません.
しかし、複素数まで範囲を広げるとその実態が明らかになります.
下に書きましたが微積の範囲を超えるので読みたい人だけ読んでください.
この、卵が生まれる瞬間($z=0$) ではその前後でどのようなことが起こっているでしょうか?
これは前々回の授業の中でコメントしました.
$V_c$ は $c<-1$ や、$c>0$ では、一筋の曲線だけになります.
楕円曲線(wikipedia)
も参考にしてください. 横の絵の $y^2=x^3-x+b$ の絵と対応しています.
この曲線のムーヴィーを頭の中で動かしてみてください.
そして関数の形がイメージ出来たでしょうか?
ここまでが微積の内容です.
少し書きすぎたので陰関数定理はまたどこかで書きます.
複素数に拡張する話と代数幾何の入り口
$x^2+y^2-3xy=c$ なる曲線を複素数上の方程式と思うこともできます.
つまり、$x,y\in{\Bbb C}$ として、$V^{{\Bbb C}}_c=\{(x,y)\in{\Bbb C}^2|F(x,y)=c\}$
を考えるのです.
この集合 $V^{\Bbb C}_c$ は、${\Bbb C}^2$ の中の2次元の物体
(多項式の零点集合、広くは代数多様体)です.
4次元の中の2次元ですから、よくわからないですが、実は、
この物体は4次元の中でドーナツの"表面"のような形をしています.
このとき、 さっきと比較すると、 $V_c\subset V^{\Bbb C}_c$ となり、あのデカルトの正葉線は
このトーラスの一部に描かれていることになります.
つまり、トーラスを ${\Bbb R}^2\subset {\Bbb C}^2$ なる部分空間で切った切り口と
考えてもいいでしょう.
複素数で考える利点は、実数の時は特異点としてぐちゃぐちゃしていたものが
複素数で考えるとすっきりすることがあります.
ただし、今回は、複素数として拡張してトーラスとした時も、
$c=0,-1$ のときに特異点を持っています.
$c=-1$ のときは、$x^3+y^3-3xy+1$ を複素の範囲で1次の積に分解して、
トーラスが3つの平面に分解されます.
なんとなくしたのような絵でしょうか
3つの平面なのに、3つの球面のように書かれているのは、さきほど無限遠点のために一点
除いたのと同じ理由で、3つの球面にそれぞれ3つ穴を開けてみれば、球面はそれぞれ
平面と同じようなもので出来ています.
$c=0$ では、一点で特異点(トーラスのどこかでとんがっている)です.
詳しくはどう見るんでしょうか?($c=0$で1点でつぶれるようなサイクルを
見つかるのだと思いますが、よくわかりません.
これは専門家にとってはそれほど難しいことではないはずですが深入りは避けます.)
さて、
$z=1,0,-0.5,1 $はトーラス、もしくは3つの球面、特異点のあるトーラスのどこを切ったのでしょうか?
$V_c$ は平面上の曲線でたまに変な特異点が表れていましたが、
また、この切り口 ${\Bbb R}^2$ は固定されているので、、$c$ が移り変わると、
このトーラスが ${\Bbb C}^2$ の中で動いていることにもなります.
つまり、$V_c^{{\Bbb C}}$ のムーヴィーです.
最後に、このような代数多様体は、普通はコンパクトな複素射影平面
${\Bbb C}P^2$ のような ${\Bbb C}^2$ を拡張した空間に埋め込んで見るのが
自然です.そうすると、上のような点を抜いて考えなくてもよくなる.
実特異点を単なる切り口として理解できる(場合がある)、
空間はコンパクトになるなどさまざまな利点があります.
そのような空間でさっきのトーラスを動かして見る(Lefschetz pencil)など、
このあたりで盛んに研究している人たちもいます.
このあたりのこと、複素射影平面などにについては、代数の先生に聞くか、
授業で学んでください.
これは微積分のブログですので、この辺にとどめておきます.
今日は以下の演習を行いました.
- 特異点
- 勾配ベクトル
- 陰関数定理II ($F(x_1,x_2,\cdots,x_n)=0$ の形)
- 陰関数定理III ($F(x,y,z)=G(x,y,z)=0$ の形)
以下、余計なことを書きすぎたので最後の2つについては書けませんでした。
またどこかでかきます.
次回はラグランジュの未定乗数法です.
特異点
ある方程式 $F(x_1,x_2,\cdots,x_n)=0$ を満たす点 $(x_1,x_2,\cdots,x_n)$ の中で、
$$\begin{cases}F_{x_1}(a_1,a_2,\cdots,a_n)=0\\F_{x_2}(a_1,a_2,\cdots,a_n)=0\\\cdots\\F_{x_n}(a_1,a_2,\cdots,a_n)=0\end{cases}$$
を満たす点のことを特異点といいました.
勾配ベクトル
勾配ベクトルは以前やりましたが、ここでは
関数 $F(x,y)$ $F(x,y,z)$ に対してその役割と性質をまとめておきます.
関数 $z=F(x,y)$ $w=F(x,y,z)$ があったときにその勾配ベクトルとは
$\text{grad}(F)(x,y)=(F_x(x,y),F_y(x,y))$,
$\text{grad}(F)(x,y,z)=(F_x(x,y,z),F_y(x,y,z),F_z(x,y,z))$
などとなり、それぞれ、2次元上のベクトルと3次元上のベクトルになります.
これを勾配ベクトルといいます.
また、このとき、このベクトルたちは各点に与えられているので、
そのような状況をベクトル場、この場合は関数の勾配を与えているので
勾配ベクトル場とよばれます.
この場という言葉は物理(ヒッグズ場とか重力場とか)でも出てきますが、
この場合と同じような意味合いです.
空間の上の各点に一斉に与えられる一つの状態を表しています.
例えば $f(x,y)=x^2+y^2$ の場合の $\text{grac}(f)(x,y)=(2x,2y)$ の
様子は授業でもやりましたが、以下のようになります.
放射状になっているのは、各点において関数 $f(x,y)=x^2+y^2$ が増える方向が外向きであるからです.
もう一次元落として考えれば、$f(x)=x^2$ も、導関数 $f'(x)=2x$ であり、絶対値が大きくなる
に従って2倍のスピードでその傾きが増えています.
関数の接平面の傾きがだんだんと急になっていることを表しています.
また、同心円はこれらのベクトルに一斉に直交しますがその円は $f(x,y)$ を
一定とする集合 $V_c=\{(x,y)|x^2+y^2=c\}$ となる等高線を意味します.
皆さんにやってもらったのは $f(x,y)=xy$ でしたが、
その時は以下のようになりました.
矢印をつなげて書けば
$y=-x$ の近くの点から矢印をたどっていくと、
まず、原点方向に向かって流れ、向きを変えて
今度は $y=x$ の近くの点を通って無限大に流れていきます.
これは、馬の鞍の腹の方から登っていき、背中を通って馬の頭(もしくは尻)の方を
だどって登っていくことに対応しています.
ちなみに原点では矢印が有りませんからどこにも向かいません.
止まったままです.
このような点は$F_x(a,b)=F_y(a,b)=0$ ですから、関数 $z=F(x,y)$ の
臨界点であることに注意しましょう.
授業中に等高線も描きましたね.自分でももう一度やってみてください.
関数 $w=F(x,y,z)$ においても勾配ベクトル場があります.
関数のグラフは4次元 $(x,y,z,w)$ の中に入っている3次元の物体なので見えませんが、
その等高面 $F(x,y,z)=c$ は3次元の中の曲面として見ることができます.
それは等高面なのでそれと垂直な方向に勾配ベクトルが向いています.
例えば、$F(x,y,z)=x^2+y^2+z^2$ のときは、等高面 $x^2+y^2+z^2=c$ は同心球
のことで、勾配ベクトル場は $\text{grad}(F)(x,y,z)=(2x,2y,2z)$ ですので、
上と同様一点から矢印が湧き出しています.
一般の関数 $z=F(x,y)$ や $w=F(x,y,z)$ は臨界点が複数入り乱れ、その周りで
$\text{grad}(F)$ が動き回っていることになります.
$z=F(x,y)$ において、非退化な(ヘッシアンが消えてない)臨界点の周りでの
$\text{grad}(F)$ の"様子"は上の、 $x^2+y^2$(湧き出し)もしくは、
$xy$ (馬の鞍)もしくは、$-x^2-y^2$ (吸い込み) のどれかに実はなっています.
退化した臨界点に関する臨界点では、状況は複雑で、ベクトル場を自分で
描いてみるとよくわかると思います.
以下、実際の具体例について、授業で取り上げた関数についての話です.
関数 $F(x,y)=x^3+y^3-3xy$ の話
例題6-1(1)
$F(x,y)=x^3+y^3-3xy=0$
は、デカルトの正葉線と呼ばれます.
のような集合ですが、$F_x(x,y)=3x^2-3y=0$ かつ $F_y(x,y)=3y^2-3x=0$
は、$(x,y)=(0,0)$ のみです.この点において接線が存在しないことになります.
これは、$z=F(x,y)$ の関数の $z=0$ での等高線とも考えられます.
前回の陰関数定理を用いれば $F_y=3y^2-3x\neq 0$ のとき、
つまり、$(x,y)=(0,0)$ もしくは $(\sqrt[3]{4},\sqrt[3]{2})$
以外では、各点は、その点の十分小さい周りにおいて、$x$-軸から関数の形をしている
ことがわかりました.
これは、$y$ に関する3次方程式 $y^3-3xy+x^3=0$ の解として、
この集合をみると分かるように、$x<0$ もしくは $x>\sqrt[3]{4}$ のとき、
この3次方程式は1つの実数解があり、$0<x<\sqrt[3]{4}$ のとき
3つの異なる実数解があります.
これは $x,y$ の変数を入れ替えてもおなじことです.
また、例題6-5(1) でも同じ式からなる集合
の陰関数を $y=\varphi(x)$ とし、$b=\varphi(a)$ において、
$\varphi'(a)=-\frac{F_x(a,b)}{F_y(a,b)}=-\frac{a^2-b}{b^2-a}$
であり、$\varphi'(a)=0$ となるような点は $a^2-b=0$ となり、
そのような点は $(a,b)=(0,0)$ もしくは $(\sqrt[3]{2},\sqrt[3]{4})$
となる.
例題6-4から
陰関数の臨界点での2階微分は以下のようになります.
授業では最後の方の計算を間違えていました.
$\varphi''(a)=-\frac{F_{xx}(a,b)}{F_y(a,b)}$ であるから、
$F_{xx}(x,y)=6x$より
$\varphi''(\sqrt[3]{2})=-\frac{6\sqrt[3]{2}}{3\sqrt[3]{4^2}-\sqrt[3]{2}}=-\frac{6\sqrt[3]{2}}{5\sqrt[3]{2}}=-\frac{6}{5}<0$
となりますので、$(\sqrt[3]{2},\sqrt[3]{4})$ では $x$-軸から見て極大になっている
ことがわかります.
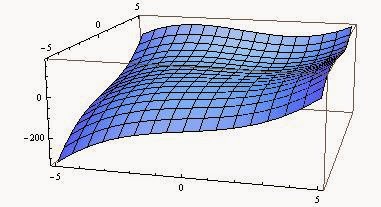
また、この関数を $z=F(x,y)$ なる関数として、グラフを作ってみると下のようになります.
なんとなく人間工学に基づいて設計された椅子のような形をしていますね.
この椅子、この絵からはよくわかりませんが、臨界点は $(0,0)$ と $(1,1)$ あります.
$(1,1)$ では極小値ですが、 $(0,0)$ ではいわゆる馬の鞍になっています.
座り心地がよさそうですね.3Dプリンターで作ってみたいくらいです.
もし家具屋でこのような曲面に出会ったら触って臨界点の位置を実感してください.
馬の鞍というのは、授業でもやりましたが、局所的に$z=xy$ となっている点です.
$z=x^2-y^2$としても定義域の座標変換で同じ形の臨界点が表れます.
そのような関数のグラフの $z=0$ での切り口は$x=0$ もしくは$y=0$ となる2つの直線です.
$F(x,y)=x^3+y^3-3xy$ の例では、$(0,0)$ の付近ではこの関数の高次の項 $x^3+y^3$ を
無視して考えます.
すると、主要項は $-3xy$ であり、大体馬の鞍だというわけです.
それが、$F(x,y)=0$ が原点で周りでクルンとなっている理由なわけです.
いまは $z=-3xy$ とは違い、3次の項のせいで、原点から遠くの方で2つの線はつながっています.
ちなみに $F(x,y)=x^3+y^3-3xy$ の勾配ベクトル場を描いて、矢印を
滑らかに繋いでやると下のようになります.
$(1,1)$ において、矢印がわき水のように湧き出していますね.
原点では局所的にさっきの $xy$ ベクトル場と同じような状況になっています.
デカルトの正葉線は関数 $z=F(x,y)$ の $z=0$ での等高線なわけですが、
この、ボールペンの試し書きのような曲線は、
他の高さではどうなっているでしょうか?
($z$ 座標は高さととらえることもできますが、時間と考えても面白いです.)
$V_c=\{(x,y)\in{\Bbb R}^2|F(x,y)=c\}$ として、$V_c$ の絵を
追いかけていきましょう.
$V_0$ は上のボールペンの試し書きでした.
$V_1$ は下のような曲線です.
交差が外れていますね.
$V_{-0.5}$ のときは下のようになります.
卵が出てきましたね.
そして $z$ をさらに下げていくと、この卵は $(1,1)$ に向かって小さくなって、
$z=-1$のときに一点になります.$F(1,1)=-1$なので、丁度極小値の時なわけです.
これは、$x^3+y^3-3xy+1=(x+y+1)(x^2+y^2-xy-y-x+1)$ のように因数分解されて、
もう一つの等高線の成分は直線になります.
$x^2+y^2-xy-y-x+1=0$ の方は、$(2x-y-1)^2+3(y-1)^2=0$ と書き直せるので、
実数の範囲では$(x,y)=(1,1)$ しかありません.
しかし、複素数まで範囲を広げるとその実態が明らかになります.
下に書きましたが微積の範囲を超えるので読みたい人だけ読んでください.
この、卵が生まれる瞬間($z=0$) ではその前後でどのようなことが起こっているでしょうか?
これは前々回の授業の中でコメントしました.
$V_c$ は $c<-1$ や、$c>0$ では、一筋の曲線だけになります.
楕円曲線(wikipedia)
も参考にしてください. 横の絵の $y^2=x^3-x+b$ の絵と対応しています.
この曲線のムーヴィーを頭の中で動かしてみてください.
そして関数の形がイメージ出来たでしょうか?
ここまでが微積の内容です.
少し書きすぎたので陰関数定理はまたどこかで書きます.
複素数に拡張する話と代数幾何の入り口
$x^2+y^2-3xy=c$ なる曲線を複素数上の方程式と思うこともできます.
つまり、$x,y\in{\Bbb C}$ として、$V^{{\Bbb C}}_c=\{(x,y)\in{\Bbb C}^2|F(x,y)=c\}$
を考えるのです.
この集合 $V^{\Bbb C}_c$ は、${\Bbb C}^2$ の中の2次元の物体
(多項式の零点集合、広くは代数多様体)です.
4次元の中の2次元ですから、よくわからないですが、実は、
この物体は4次元の中でドーナツの"表面"のような形をしています.
正確には、無限遠点に伸びていますので、ドーナツの表面の一点を
抜いたような形状をしています.
ドーナツとはこのようなリング状の甘いお菓子の総称ですから、
ドーナツではまずくって、このような形状のことを数学ではトーラスといいます.
このとき、 さっきと比較すると、 $V_c\subset V^{\Bbb C}_c$ となり、あのデカルトの正葉線は
このトーラスの一部に描かれていることになります.
つまり、トーラスを ${\Bbb R}^2\subset {\Bbb C}^2$ なる部分空間で切った切り口と
考えてもいいでしょう.
複素数で考える利点は、実数の時は特異点としてぐちゃぐちゃしていたものが
複素数で考えるとすっきりすることがあります.
ただし、今回は、複素数として拡張してトーラスとした時も、
$c=0,-1$ のときに特異点を持っています.
$c=-1$ のときは、$x^3+y^3-3xy+1$ を複素の範囲で1次の積に分解して、
トーラスが3つの平面に分解されます.
なんとなくしたのような絵でしょうか
$c=-1$ に近づいたときにトーラスが変形して3つの成分に分かれる図
3つの平面なのに、3つの球面のように書かれているのは、さきほど無限遠点のために一点
除いたのと同じ理由で、3つの球面にそれぞれ3つ穴を開けてみれば、球面はそれぞれ
平面と同じようなもので出来ています.
$c=0$ では、一点で特異点(トーラスのどこかでとんがっている)です.
詳しくはどう見るんでしょうか?($c=0$で1点でつぶれるようなサイクルを
見つかるのだと思いますが、よくわかりません.
これは専門家にとってはそれほど難しいことではないはずですが深入りは避けます.)
さて、
$z=1,0,-0.5,1 $はトーラス、もしくは3つの球面、特異点のあるトーラスのどこを切ったのでしょうか?
$V_c$ は平面上の曲線でたまに変な特異点が表れていましたが、
また、この切り口 ${\Bbb R}^2$ は固定されているので、、$c$ が移り変わると、
このトーラスが ${\Bbb C}^2$ の中で動いていることにもなります.
つまり、$V_c^{{\Bbb C}}$ のムーヴィーです.
最後に、このような代数多様体は、普通はコンパクトな複素射影平面
${\Bbb C}P^2$ のような ${\Bbb C}^2$ を拡張した空間に埋め込んで見るのが
自然です.そうすると、上のような点を抜いて考えなくてもよくなる.
実特異点を単なる切り口として理解できる(場合がある)、
空間はコンパクトになるなどさまざまな利点があります.
そのような空間でさっきのトーラスを動かして見る(Lefschetz pencil)など、
このあたりで盛んに研究している人たちもいます.
このあたりのこと、複素射影平面などにについては、代数の先生に聞くか、
授業で学んでください.
これは微積分のブログですので、この辺にとどめておきます.









0 件のコメント:
コメントを投稿