[場所オンライン(月曜日3限)]
今回は、連結性と弧状連結性についてやりました。
連結性
位相空間が連結であることは前回定義しました。
定義10.3
位相空間 $X$ が空でも $X$ でもない開集合 $U,V$
を用いて、$X=U\sqcup V$ と表せないとき、 $X$ は
連結といい、$X$ が連結ではないとき
$X$ は不連結という。
この定義を次のように言い換えることができます。
定理10.6
$X$ が連結であることは、$X$ の開かつ閉集合は $X$ もしくは
$\emptyset$ のみであることと同値である。
となる。
連結集合について定義しておきます。
定義11.1
$(X,\mathcal{O})$ を位相空間とする。
$A\subset X$ が連結集合であるとは、相対位相
$(A,\mathcal{O}_A)$ が連結空間であることとして
定義する。
つまり、このことは言い換えれば、
任意の開集合 $U,V\in \mathcal{O}$ に対して、
$A\subset U\cup V$ かつ
$A\cap U\cap V=\emptyset$
なら、$A\subset U$ もしくは $A\subset V$
ということになります。
これは、
$(A\cap U)\cup(A\cap V)=A$ であることは、$A\subset U\cup V$ と同値
$(A\cap U)\cap (A\cap V)=\emptyset$ であることは $A\cap U\cap V=\emptyset$ と同値
$A\cap U=A$ であることは $A\subset U$ と同値
$A\cap V=A$であることは $A\subset V$ と同値
であることからわかります。
最終的に、$A\subset U$ もしくは $A\subset V$ が成り立つのですが、
このうちどちらかしか成り立ちません。
いくつかの例の前に以下を示しておきます。
定理11.1
$({\mathbb R},\mathcal{O}_{d_1})$ は連結である。
(証明) ${\mathbb R}$ が連結でないとします。
${\mathbb R}=U\sqcup V$ となる空ではない開集合 $U,V$ が
存在することになります。
$a\in U$ かつ $b\in V$ をとり、
$a<b$ としておきます。もしそうでなかったら、$U,V$ の役目を入れ替えれば
実現出来ます。
$c=\sup\{x\in U|x\le b\}$
とおきましょう。
このとき、$\epsilon >0$ が存在して、$B_{d_1}(c,2\epsilon )\subset U$ となります。
しかし、$c+\epsilon\in U$ であり、$c+\epsilon<b$ であることから、
$c=\sup\{x\in U|x\le b\}$ であることに反します。
よって、$c\in V$ ということになります。
同様に、$\delta>0$ が存在して、$B_{d_1}(c,\delta)\subset V$ となり
$(c-\delta,c]\subset V$ が成り立ちます。
これは、$c$ が$\{x\in U|x\le b\}$ の上限であることに反します。
もし上限であるなら、$\forall \epsilon>0$ に対して、$c-\epsilon <x\le c$
となる$x\in U$ が存在するからです。
よって $c$ は $U,V$ のどちらも含まれないので ${\mathbb R}=U\cup V$
であることに反します。
よって、${\mathbb R}$ が連結になるということになります。$\Box$
ここで次の定理を示しておきましょう。
定理11.2
$X,Y$ を位相空間とする。$f:X\to Y$ を全射連続写像とする。
$X$ が連結なら $Y$ も連結である。
(証明) $U\subset Y$ を開かつ閉集合とします。
このとき、$f^{-1}(U)$ も開かつ閉集合です。
$X$ は連結なので
$f^{-1}(U)=\emptyset$ か $f^{-1}(U)=X$ となります。
$Y$ が全射であることから、$U=\emptyset$ もしくは $Y$ となります。
これは $Y$ が連結であることを意味します。$\Box$
このことから、$f$ が全射でなくても、$X$ が連結なら
$f(X)$ も連結であることが分かります。
また、$A\subset X$ が連結集合であるなら、$f(A)$ は連結
ということになります。
つまり、
連結集合の連続写像による像(連続像といいます)は連結ということになります。
このことから、連結性は位相的性質になることも分かります。
なぜなら
$f:X\to Y$ が同相であるとします。
このとき、$X$ が連結とすると、定理11.2から $Y$ も連結になります。
よって、連結性は位相的性質になるからです。
次の定義をしましょう。
定義11.2
$a\in X$ に対して、$a$ を含む連結集合の内最大のものを
$a$ の連結成分といい、$C_X(a)$ と書く。
また簡単に $C(a)$ と書くこともある。
$a\sim x$ は同じ連結成分に属するとして $X$ 上に同値関係を定めることができます。
そうすると、
$X$ のこの同値関係の同値類によって、分解
$$X=\sqcup_{\lambda\in \Lambda}C_X(a_\lambda)$$
を与えることができます。
これを連結成分分解といいます。
$X$ が連結であることは、$X=C_X(a)$
のように$X$ の任意の元がただ1つの連結成分に属することと同値になります。
ここで次の定理を示しておきます。
命題11.2
$A\subset X$ が開かつ閉集合であれば、
$A$ は $X$ の連結成分のいくつかの和集合となる。
(証明) $A$ が開かつ閉集合とします。このとき、
$\forall a\in A$ に対して、$A\cap C_X(a)\subset C_X(a)$
より、$A\cap C_X(a)$ は $C_X(a)$ の開かつ閉集合になります。
$C_X(a)$ は連結であり、$a\in A\cap C_X(a)$ は空ではないから
$A\cap C_X(a)=C_X(a)$ となります。
よって、$C_X(a)\subset A$ ととなり、よって、$\forall a\in A$ に対して、$C_X(a)\subset A$ であるから
$\cup_{a\in A}C_X(a)\subset A$ また、$A\subset \cup_{a\in A}C_X(a)$
であるから
$$A=\cup_{a\in A}C_X(a)$$
となり、$A$ はいくつかの連結成分の和集合となります。$\Box$
この証明の途中で用いたことを復習しておきます。
相対位相の閉集合について
$A\subset X$ での相対位相において、
$A$ における開集合は $X$ の開集合 $U$ を用いて $A\cap U$ と書き表されます。
(証明) $A$ における閉集合 $F$ は、$A-F=A\cap F^c$ より $A$ における開集合だから、
$A\cap F^c=A\cap U$ となる $X$ の開集合 $U$ が存在します。
よって、この補集合を取ると、
$A^c\cup F=A^c\cup U^c$
$A^c\cap F=\emptyset$ であるから、$A^c$ の部分を取ると、
$F=(A^c\cup U^c)\cap A=(A^c\cap A)\cup (U^c\cap A)=A\cap U^c$
よって、$A$ 上の閉集合は、$X$ のある閉集合 $G$ を用いて、
$A\cap G$ とかけることがわかります。
次の定理を示しましょう。
定理11.4
連結集合 $A$ に対して、$A\subset B\subset \overline{A}$
を満たす任意の集合 $B$ は連結である。
(証明) $B\subset U\cup V$ を満たす $X$ の開集合
が $B\cap U\cap V=\emptyset$ を満たすとします。
このとき、
$B\cap U\neq \emptyset$ を満たすと仮定します。
このとき、 $B\subset \overline{A}$ であるから
$\overline{A}\cap U\neq \emptyset$ です。
$x\in\overline{A}\cap U$ をとります。
このとき、$U$ は開集合だから $U\in \mathcal{N}(x)$ となります。
よって、$A\cap U\neq \emptyset$ を満たします。
$A$ は連結だから、
$A\subset U\cup V$ かつ $A\cap U\cap V=\emptyset$ より
$A\subset U$ もしくは $A\subset V$ です。
しかし、$A\cap U\neq \emptyset$ であるから $A\subset U$ です。
よって、$A\cap V=\emptyset$ であるから $\overline{A}\cap V=\emptyset$
である。つまり、$B\cap V=\emptyset$ です。
このことから、$B\subset U$ が分かります。
また、$B\cap V\neq \emptyset$ である場合からも、
同じように $B\subset V$ が証明することができます。$\Box$
この定理から次が成り立ちます。
定理11.5
任意の $a\in X$ に対して、連結成分 $C(a)$ は閉集合である。
(証明) $C(a)\subset \overline{C(a)}$ が成り立つ。
また定理11.4から $\overline{C(a)}$ は連結になります。
連結成分の最大性により、$\overline{C(a)}\subset C(a)$
が成り立ちます。この包含関係から、
$C(a)=\overline{C(a)}$ が成り立つ、つまり $C(a)$ が閉集合になります。
例
$(a,b)\subset {\mathbb R}$ は ${\mathbb R}$ と同相であるから、
連結は位相的性質なので、$(a,b)$ も連結性になります。
この閉包 $[a,b]$ も同相になります。
命題11.3
$\forall r\in {\mathbb Q}$ に対して、$r$ の連結成分 $C(r)$ について
$C(r)=\{r\}$ が成り立ちます。
(証明) $\forall r,s\in {\mathbb Q}$ に対して、
$r<s$ に対して、$r<q<s$ となる無理数 $q$ が存在して、
${\mathbb Q}\cap (-\infty,q)={\mathbb Q}\cap (-\infty,q]$
は開かつ閉集合であるから、${\mathbb Q}\cap (-\infty,q]$ は
連結成分の和集合つまり、$C(r)\subset {\mathbb Q}\cap (-\infty,q]$
であり、
同様に、$C(s)\subset {\mathbb Q}\cap [q,\infty)$
であるから、$C(r)\cap C(s)=\emptyset$ であるから、
$\forall r\in{\mathbb Q}$ の連結成分は $r$ のみとなります。$\Box$
このように、$\forall a\in X$ に対して、$C_X(a)=\{a\}$
であるとき、$X$ は完全不連結であるという。
よって、$({\mathbb Q},\mathcal{O}_{d_1})$ は完全不連結であり、
ゾルゲンフライ直線 $({\mathbb R},\mathcal{O}_{l})$ も完全不連結となります。
また、連結性の最後に中間値の定理を示しました。
定理11.6
位相空間 $X$ と連続関数 $f:X\to {\mathbb R}$ をとる。
$X$ の連結な部分集合 $A$ に対して、
$a,b\in A$ が $f(a)<f(b)$ を満たすとする。
このとき、$f(a)<\forall c <f(b)$ となる $c$ に対して、
$f(x)=c$ となる $x\in A$ が存在する。
(証明)$A$ は連結なので、$f(A)\subset {\mathbb R}$ も連結であり、
$f(a),f(b)\in f(A)$ が成り立ちます。
よって、このとき、$f(a)<c<f(b)$ が $f(x)=c$ となる $x$ が存在しないとする。
このとき、$B=f(A)\cap (-\infty, c)=f(A)\cap (-\infty ,c]$ より、
$B$ は空でも全体でもない $f(A)$ の開かつ閉集合であるから矛盾する。
よって、$f(x)=c$ となる $x\in A$ が存在する。$\Box$
弧状連結性
弧状連結の定理をしましょう。
定義11.4
位相空間 $X$ が弧状連結であるとは以下を満たすことを意味します。
$\forall a,b\in X$ に対して、ある連続写像 $f:I\to X$ が
存在して、$f(0)=a$ かつ $f(1)=b$ を満たす。
ここで、$I$ は閉区間 $[0,1]$ です。
すぐにわかるのは次の定理です。
定理11.7
弧状連結なら連結である。
(証明)$X$ が弧状連結であるとします。
このとき、$\forall a,b \in X$ に対して、連続写像 $f:I\to X$ が存在して
$f(0)=a$ かつ $f(1)=b$ を満たし、つまり、$a,b\in f(I)\subset X$ を満たします。
$I$ が連結であるから、$f(I)$ も連結になり、$f(I)\subset C(b)$ であるから
$a$ は $b$ の連結成分に属します。
つまり、$a\in C(b)$ であり、つまり $X\subset C(b)$ より
$X=C(b)$ となります。つまり $X$ は連結となります。$\Box$
この定理の逆は一般には成り立ちません。
つまり、連結だが、弧状連結であるものが存在します。
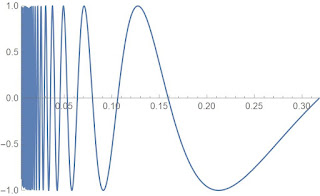
定理11.8
$J=\left\{\left(x,\sin\frac{1}{x}\right)|x\in {\mathbb R}_{>0}\right\}$
とし、
$I=\{(0,t)|-1\le t\le 1\}$
とする。このとき $X=I\cup J$ は連結であるが、弧状連結ではない。
$J$ は下の図のようなグラフになっており、
$I$ はこの $y$ -軸の $[-1,1]$ の区間です。
(証明)連結性について
$J$ は ${\mathbb R}_{>0}$ 上の連続関数 $\sin \frac{1}{x}$ のグラフであり
連続像になります。よって、定理11.2から $J$ は連結。
また、$\forall (0,t)\in I$ に対して、数列 $\left(\frac{1}{2n\pi+\text{arcsin}t},t\right)$
は、$J$ 上の点列であり、$n\to \infty$ において $(0,t)$ に収束するので、
$(0,t)\in \overline{J}$ となります。
これは、$I\cup J\subset \overline{J}$ であることを示しており、
$$I\subset I\cup J\subset \overline{J}$$
から、定理11.4 から $X=I\cup J$ も連結ということになります。
非弧状連結について
$O\in X$ を ${\mathbb R}^2$ の原点とし $A=(\frac{1}{\pi},0)$ がある連続写像
$f:I\to X$ によって $f(0)=O$ かつ $f(1)=A$ とならないことを示します。
もし結べるとすると、連続写像 $f:[0,1]\to X$ が存在して、
$f(0)=O$かつ $f(1)=A$ を満たします。
そうすると、今、$f^{-1}(O)=0$ と仮定しておきます。
このとき、
$B_{d_2}(O,\frac{1}{2})$をとり、
$0\in f^{-1}(B_{d_2}(O,\frac{1}{2}))$ の近傍$[0,\delta)$ が存在して、
$[0,\delta)\subset f^{-1}(B_{d_2}(O,\frac{1}{2}))$を満たします。
ここで、$B$ は下の円の内側になります。
そうすると $f^{-1}(O)=0$ と仮定したことから $\text{pr}_1(f([0,\delta)))=[0,a)$ となる
$a>0$ が存在します。
よって、$\frac{2}{(4n+1)\pi}<a$ を満たす$n$ が存在し、
$(\frac{2}{(4n+1)\pi},1)\in f([0,\delta))\subset B$ を満たします。
しかし、$(\frac{2}{(4n+1)\pi},1)\not\in B$ であるので、
矛盾します。
よって、$X$ は弧状連結ではないということになります。$\Box$
途中で、$f^{-1}(O)=0$ と仮定しましたが、
これは簡単に証明できます。$\{t\in I|f(t)=O\}$ となるものの
$\sup$ を $t_0$ を取り、$[t_0,1]$ を $[0,1]$ に線形に引き伸ばしたものを
$f$ に合成したものを再び $f$ とおけば良いです。

0 件のコメント:
コメントを投稿